Les mondes à plusieurs dimensions: les enjeux de la transmission de connaissances mathématiques dans la fiction (Flatland, Edwin A. Abbott)

Un des enjeux de la réflexion sur le rôle des sciences humaines et sociales dans la transmission du savoir est d’interroger les modalités particulières de cette transmission et leur influence sur la constitution du savoir en tant que tel. La manière dont est transmis un savoir, selon des contextes historiques, culturels, idéologiques et politiques variés, exerce autant sinon plus d’influence que ce savoir lui-même, comme l’a très bien montré McLuhan dans son ouvrage Pour comprendre les médias : les prolongements technologiques de l’homme en affirmant : « Le médium, c’est le message » (McLuhan, 2000).

Le savoir mathématique peut-il alors trouver une modalité d’expression qui fasse justice à ses enjeux épistémiques à travers une œuvre de littérature ? Pour le dire autrement, peut-on trouver une langue commune entre sciences et littérature ? C’est la question que se pose l’épistémocritique, champ de recherche qui vise à étudier l’insertion de savoirs à l’intérieur de la littérature et qui voit le jour sous les années 1980, sous l’impulsion de Michel Pierssens qui en pose le cadre théorique dans son ouvrage Savoirs à l’œuvre – Essais d’épistémocritique (Pierssens, 1990). Pierssens s’aventure dans des œuvres qui accueillent ces croisements entre différents savoirs et approches de ces savoirs, et introduit un certain nombre de concepts opératoires (agents de transfert, greffes épistémiques, figures épistémiques, etc.) qui vont permettre à l’épistémocritique de structurer son approche méthodologique. À sa suite, Laurence Dahan-Gaida dans son article « L’épistémocritique : problèmes et perspectives » (Minary, 2001) montre que l’analyse des idées scientifiques présentes à l’intérieur des textes littéraires ne peut se limiter au simple relevé de celles-ci. Bien au contraire, il s’agit selon elle de dégager des rapports de détermination réciproque, et il faut pour cela considérer que l’œuvre littéraire permet la co-constitution des discours littéraires et scientifiques à partir de leur rencontre : aucun des deux ne se contente de redoubler ou de refléter l’autre. Plus récemment, Patrick Marot dans L’inscription littéraire des savoirs (Marot, 2019) suggère de parler d’« idiologues » pour aborder l’insertion d’un régime épistémique dans une œuvre littéraire en défendant l’idée qu’un savoir n’est jamais un élément tout à fait exogène dans une œuvre, mais est systématiquement incorporée par celle-ci à l’aide d’un certain nombre d’outils, au nombre desquels il évoque les dispositifs visuels. Notre analyse s’appuie sur l’ensemble de ces travaux pour développer une approche interdisciplinaire qui prend en compte la part du visuel pour analyser la manière qu’a la littérature d’aborder, de vulgariser et même d’explorer des connaissances mathématiques assez pointues dans l’œuvre Flatland d’Edwin A. Abbott.

Edwin Abbott Abbott est un mathématicien et théologien anglais, directeur de la City of London School, qui publie Flatland dans la seconde moitié du XIX^e siècle en 1884. C’est l’occasion pour lui d’aborder la question de l’existence de dimensions supérieures à la nôtre, dans un monde fictif aux tonalités satiriques, qui ne se prive pas de remettre en question certains principes de l’organisation de la société victorienne de son époque. Abbott y développe une approche didactique fondée sur des raisonnements mathématiques et analogiques, qui sert un propos à la fois épistémique et religieux. Il s’agit en effet d’une œuvre de fiction qui met en scène un carré nommé A. Square qui évolue dans un monde à deux dimensions, Flatland, peuplé par des figures géométriques telles que des lignes, des carrés, des pentagones, des hexagones, ou encore des ronds. La première partie de l’ouvrage s’intéresse aux us et coutumes de ce pays imaginaire et en explique notamment l’organisation politique, architecturale, le système de classes qui la régit puisque plus on a de côtés dans Flatland, plus on est haut placé dans la hiérarchie – les ronds sont ainsi considérés comme le summum de l’échelle sociale et sont affectés à des fonctions religieuses. La seconde partie met en scène l’arrivée d’une Sphère, donc une figure à trois dimensions, au milieu du salon d’A. Square, qui vient enlever le personnage principal pour lui faire visiter d’autres mondes : celui à zéro dimension, peuplé uniquement par un point égocentrique et narcissique, celui à une dimension, et celui bien sûr à trois dimensions, dans l’espoir que le carré puisse transmettre à son tour son savoir de retour sur Flatland. Bien sûr, ce savoir sera considéré comme hérétique et A. Square condamné à une fin funeste.

À partir de cette œuvre, nous aimerions montrer comment s’organise la transmission du savoir dans un texte de fiction, puisqu’elle s’opère à deux niveaux : les explications que la Sphère adresse au Carré, et celles que l’œuvre de manière générale adresse à ses lecteurs. Nous verrons que cette transmission qui repose sur une vulgarisation de la théorie des mondes à plusieurs dimensions réalise ainsi une double adresse qui s’appuie sur des outils bien distincts, allant du raisonnement analogique à l’imagination diagrammatique. Nous terminerons en évoquant les enjeux scientifiques et religieux liés à la création de cet univers. En effet, outre l’aspect plaisant et décalé, pourquoi vouloir parler des mondes à plusieurs dimensions dans un texte de fiction ? Flatland ne transmet pas seulement des outils qui permettent d’envisager quels problèmes pourraient poser des mondes à n dimensions à notre représentation, mais porte également une réflexion qui dépasse le savoir mathématique.

1. Expliquer les mondes à plusieurs dimensions dans un texte littéraire : la transmission du savoir intradiégétique

C’est l’enjeu principal de cette œuvre : comment faire comprendre, envisager et visualiser l’existence de dimensions supérieures à celles du monde dans lequel on évolue ? Cela constitue un véritable saut épistémique, un pas de côté dans la représentation du monde qui nous entoure. A. Square, le personnage principal de notre œuvre, va y être en quelque sorte préparé en amont par un rêve étrange qu’il va faire l’avant dernier jour de l’an 1999 de ce monde. Ce rêve constitue l’ouverture de la seconde partie de l’œuvre intitulée « Other worlds ». A. Square y fait la rencontre du roi d’un monde à une dimension, Lineland :

It seemed that this poor ignorant Monarch – as he called himself – was persuaded that the Straight Line which he called his Kingdom, and in which he passed his existence, constituted the whole of the world, and indeed the whole of Space. Not being able either to move or to see, save in his Straight Line, he had no conception of anything out of it (Abbott, 2007, p.44)¹.

On y apprend deux choses : l’imagination semble initialement bornée à l’espace (au sens mathématique) dans lequel évolue l’individu, et la compréhension des dimensions supérieures semble rencontrer dans un premier temps le problème de la perception. C’est parce que le roi n’est pas capable de se déplacer ou de voir dans la seconde dimension qu’il n’est pas capable de la concevoir, de l’envisager, de la comprendre ou de l’imaginer. Nous retrouvons un problème similaire soulevé en préface où le narrateur A. Square relève un certain nombre d’objections récurrentes qui lui ont été faites par les habitants de son monde à deux dimensions, parmi lesquelles l’injonction à « mesurer » ou à indiquer la direction de la nouvelle dimension qu’il évoque. C’est bien là l’un des premiers obstacles : avec quels outils (quels mots, quels instruments de mesure, quelles techniques de visualisation) parler de ce qu’on ne peut ni percevoir, ni concevoir, ni expérimenter ? Quand il s’agit d’expliquer au roi de Lineland en quoi consiste la deuxième dimension, A. Square se heurte à bien des difficultés : les mots qu’il emploie n’existent pas à Lineland qui ne connait pas les concepts de « droite » et de « gauche ». Les gestes qu’il fait, comme se décaler sur le côté et donc sortir du monde de Lineland, demeurent eux aussi inefficients puisque les habitants de Lineland ne peuvent voir que ce qui se situe sur la ligne de leur monde, et si l’on se trouve à droite de cette ligne par exemple, on « disparaît » tout simplement. Tant et si bien que face à ces différentes tentatives de démonstration et d’explication, le monarque conclut irrémédiablement par le constat que son interlocuteur n’est pas « a Man of sense », un « homme de raison » mais simplement un magicien qui dispose d’un tour de disparition et use d’un langage incohérent.

Un second « seuil » avant la révélation du personnage de la sphère va en quelque sorte préparer le terrain de la compréhension d’A. Square. C’est celui du raisonnement analogique, et plus précisément du passage par l’algèbre. Quelques minutes avant que la sphère apparaisse dans son salon, A. Square consacrait un peu de temps à son fils, un brillant petit hexagone, pour lui faire réviser des problèmes mathématiques. Or celui-ci a l’intuition, en passant par l’élévation aux puissances, de ce que pourrait être une troisième dimension :

Well, then, if a Point by moving three inches, makes a Line of three inches represented by three; and if a straight Line of three inches, moving parallel to itself, makes a Square of three inches every way, represented by three-to-the-second; it must be that a Square of three inches every way, moving somehow parallel to itself (but I don't see how) must make Something else (but I don't see what) of three inches every way – and this must be represented by three-to-the-third (Abbott, 2007, p. 51)².

Il est intéressant de remarquer ici que son raisonnement s’appuie également sur une projection dans l’espace (il utilise le verbe « moving ») qui serait toujours la même : un objet d’une dimension n+1 s’obtient en translatant un objet de la dimension immédiatement inférieure. Pour cela, il faut garder la trace du déplacement de l’objet dans la dimension précédente. Nous gardons en tête cette idée pour notre second point puisque nous verrons qu’elle est plus évidente lorsqu’elle est représentée visuellement par un tracé – et c’est ainsi qu’elle est expliquée au lecteur. Nous proposons ici un petit aperçu visuel de l’explication que donne le petit fils d’A. Square :

Figure 1 : Passage d'une dimension à une autre par translation de l'objet

À l’intérieur de l’intrigue, nous avons donc pu observer qu’il y a plusieurs événements qui viennent préparer en quelque sorte la compréhension d’A. Square et faciliter la réception de la révélation de la sphère : le rêve tout d’abord qui permet au personnage d’expérimenter la position de celui qui détient le savoir, celui précisément de l’existence d’une dimension qui n’est pas perceptible par les sens de certains personnages, et surtout qui se heurte à l’impossibilité de communiquer un tel savoir, que ce soit par la parole, l’exemple ou le raisonnement. Ses démonstrations théoriques comme expérimentales et concrètes se soldent par de cuisants échecs puisque les habitants de Lineland ont d’autres manières d’expliquer ou de percevoir un même donné. Le calcul algébrique fait également signe vers l’existence d’un inconnu théorisable, mais A. Square se refuse à lui accorder une quelconque validité même hypothétique sans expérience de première main.

La première étape, dans la transmission de ce savoir mathématique de la Sphère à A. Square, va être précisément cette expérience de première main, qui confine à une forme de révélation mystique. En effet, la Sphère apparaît au milieu du salon, au moment où le dernier grain du sablier du temps de l’an 1999 de l’ère flatlandienne tombe. Elle va tenter d’expliquer au Carré quelle est exactement sa véritable nature, en rencontrant à nouveau toutes les difficultés que nous avons évoquées précédemment puisqu’elle utilise un vocabulaire et des désignations qui restent relativement obscures pour les habitants de Flatland : « It is up above and down below » (Abbott, 2007, p.53)³ (dans un monde à deux dimensions, la hauteur n’existe pas, et les mots qui la désignent renvoie à une réalité qui n’est pas expérimentée au quotidien). À la section 17, la Sphère décide donc de passer aux « actes » comme elle le dit elle-même, afin de proclamer la vérité. Pour avoir accès au savoir de la troisième dimension, il ne faut donc pas voir un objet de la troisième dimension si l’on conserve un regard identique, mais bien modifier son regard même. Dans cette section, A. Square va contempler son propre monde, Flatland, depuis une hauteur à laquelle la sphère l’a surélevé. Il regarde des éléments dont il a déjà la connaissance, depuis une perspective qui lui est nouvelle, et c’est ce qui va lui permettre de comprendre véritablement, d’embrasser du regard et de la connaissance ce savoir nouveau. A la lecture de Flatland, on peut se demander pourquoi ce n’est pas la Sphère qui se charge elle-même de transmettre la révélation aux membres du conseil ou aux autres flatlandiens, en usant des mêmes procédés qu’elle l’a fait avec A. Square. Il nous semble que la réponse tient véritablement dans cette idée d’une conversion du regard : c’est moins l’objet nouveau qui compte, que la manière de le regarder. C’est que l’on peut voir un élément nouveau sans en tirer une connaissance nouvelle, puisqu’étant dans l’incapacité de le voir correctement, de le comprendre. Il est même possible de pouvoir démontrer quelque chose d’incompréhensible, c’est le cas lorsque les personnages passent par la démonstration purement mathématique. La section 19 propose à ce titre une représentation visuelle de ces deux visions possibles d’un même objet : une vision (2) qui ne comprend pas l’objet en question (c’est celle d’A. Square dans ses premières rencontres avec les solides puisqu’ils les considère comme des figures irrégulières), et une vision (1) du même objet mais vu différemment, les pointillés faisant signe vers une compréhension des notions de profondeur et une anticipation de ce qui ne peut pas a priori être vu selon cet angle.

Figure 2 : Un solide représenté de deux façons, selon une perspective spacelandienne et selon un point de vue flatlandien (Abbott, 2007, p. 64)

À l’issue de cette transmission, nous pouvons nous demander ce que devient ce savoir une fois acquis. Quel usage va en faire A. Square, et surtout, comment va-t-il grandir en lui et évoluer ? Ce qui va suivre l’acquisition définitive du savoir est, selon les propres mots d’A. Square, une véritable chute. Le personnage échoue en effet dans un premier temps à transmettre ses connaissances à son petit-fils hexagone qui en avait pourtant eu l’exacte intuition mathématique avant que la Sphère n’apparaisse dans le salon. Il rencontre les mêmes difficultés lors de son procès face au Haut Conseil, et finit sa vie dans une prison, à répéter perpétuellement la phrase « Upward, not Northward » pour se rappeler des explications de la Sphère. Cette affirmation perd peu à peu son sens scientifique et devient une véritable litanie dépourvue de toutes ses vertus incantatoires : le narrateur se cantonne à la répétition de mots privés de sens. Ce qui devient à présent un précepte asserte une fois encore l’idée que les mots seuls sont tout à fait incapables de transmettre la complexité de la pensée qu’ils désignent. « Vers le haut et non pas vers le Nord » devient peu à peu un vers poétique, un élan lyrique qui est savouré pour ses sons, et non plus un savoir mathématique. Flatland nous offre le récit savoureux de la transmission d’un savoir mathématique sur les mondes à plusieurs dimensions qui est un véritable échec pour le personnage principal. C’est loin d’être le cas pour les lecteurs de l’œuvre, qui sont eux-aussi à leur manière les disciples de la Sphère, et nous allons à présent voir comment.

2. La transmission du savoir au lecteur : passer par la fiction et le visuel

Dès la couverture, nous comprenons que nous sommes invités en tant que lecteur à suivre le même cheminement que le protagoniste principal de l’œuvre, c’est-à-dire, explorer les mondes à plusieurs dimensions.

Figure 3 : L'illustration de la couverture de Flatland (Abbott, 2007, p.3)

De la même manière qu’A. Square est familier des mondes à zéro, une et deux dimensions, nous sommes familiers de ce qui est désigné comme « Spaceland » et qui est en fait notre monde tel que nous l’expérimentons, un monde à trois dimensions. Sur l’illustration de la couverture, on voit apparaitre la quatrième, la cinquième, la sixième, la septième, la huitième, la neuvième et même la dixième dimension, cachées dans un gros nuage sur lequel est couché le titre de l’œuvre. L’œuvre elle-même, dont A. Square se fait passer pour l’auteur, est dédiée aux habitants de Spaceland, et leur souhaite dans son adresse : « So the Citizens of that Celestial Region May aspire yet higher and higher To the Secrets of FOUR FIVE or EVEN SIX Dimensions » (Abbott, 2007, p.4)⁴. Il y a donc une leçon, ou plutôt un raisonnement analogique, à tirer de ce récit : ce qu’expérimente A. Square dans son approche d’un monde à n+1 dimensions par rapport au sien, correspond à ce que nous pourrions expérimenter dans nos expériences de pensée visant à imaginer des mondes à n+1 dimensions par rapport au nôtre. Il y a donc un pari qui est fait à l’entrée de l’œuvre : celui que la fiction est capable de nous accompagner et de nous guider dans notre découverte d’un nouveau savoir. Allons même plus loin : elle est capable de baliser notre pensée par le biais du raisonnement analogique. Au seuil de la lecture de Flatland, ces différents éléments (la couverture, l’adresse) sont autant d’invitations à dégager une structure commune entre le monde de la fiction et notre monde, à essayer de faire correspondre un ensemble de relations qui se tissent dans l’un à celles qui se tissent dans l’autre.

À l’intérieur du texte de fiction, Abbott emploie plusieurs autres outils qui facilitent la transmission du savoir aux lecteurs. Flatland fait un usage particulier des dialogues : les personnages n’hésitent pas à accompagner leur interlocuteur dans l’acquisition du savoir qu’ils souhaitent lui transmettre, par le biais de questions/réponses. Il s’agit toujours de partir de connaissances communes pour amener progressivement, par l’analogie, par le raisonnement déductif, à étendre le champ des connaissances vers une nouvelle considération. Le discours de la Sphère ressort souvent de la maïeutique, visant à faire « accoucher » l’esprit de son interlocuteur, persuadé qu’il dispose en lui de toutes les connaissances lui permettant d’envisager un monde à trois dimensions. Mais il y a un dialogue en particulier qui attire notre attention : celui de la section 19, qui met en scène l’élève qui dépasse le maître. En effet, à ce moment-là, A. Square a terminé sa formation en quelque sorte, il a acquis le savoir que souhaitait lui transmettre la Sphère. Il s’adresse alors à elle pour lui demander de lui montrer à présent les secrets de la quatrième dimension. Nous découvrons alors que la Sphère est incapable de poursuivre le raisonnement analogique dont elle a été l’instigatrice et d’envisager à son tour un monde dont le nombre de dimensions excède celles qu’elle peut percevoir : « There is no such land. The very idea of it is utterly inconceivable⁵ » (Abbott, 2007, p. 67). Pourtant, A. Square reproduit à nouveau toutes les étapes du raisonnement mathématique qui mènent inexorablement vers l’existence d’une dimension encore supérieure, mais la Sphère réfute radicalement l’examen de cette hypothèse. Pour le lecteur, ce dialogue est évidemment une invitation à envisager par lui-même la possibilité d’une quatrième dimension, et à condamner l’attitude réfractaire de la Sphère au même titre qu’elle-même condamnait la fermeture d’esprit des créatures de Flatland, incapable d’imaginer le monde de Spaceland. Nous l’avons déjà remarqué, Flatland fonctionne comme un conte qui repose sur la répétition des mêmes situations, des mêmes dialogues, avec des permutations dans les rôles entre les sachants et les ignorants. À la manière d’un conte, l’œuvre nous offre une morale sous la forme d’une attitude épistémique à adopter : celle de ne pas immédiatement réfuter un savoir qui nous semble dans un premier temps bouleverser nos représentations du monde.

Si, comme nous l’avons vu, la Sphère refuse de poursuivre ce raisonnement pour la quatrième dimension, ou A. Square finit par oublier ce que signifie « Upward, not Northward », c’est peut-être également qu’il leur manque à tous deux des outils permettant de faciliter ces représentations et les raisonnements qui en découlent. En effet, lorsque le lecteur assiste aux incompréhensions successives des différents personnages, il ne faut pas oublier qu’il a accès, lui, à des représentations diagrammatiques qui viennent appuyer sa propre compréhension des enjeux qui lui sont présentés. Nous nous proposons ici d’esquisser rapidement une définition opératoire de ce que nous entendons par diagramme. Nous nous appuyons pour cela sur les travaux de Charles Sanders Peirce qui définit le diagramme par la relation iconique qu’il entretient avec l’objet représenté (Peirce, 1931). Le diagramme entretient un rapport de similarité avec l’objet qu’il représente (par opposition à un rapport de contiguïté, qui définit une relation indicielle, et un rapport conventionnel, qui définit une relation symbolique). Cette similarité doit se lire dans les relations des parties entre elles et avec le tout : ainsi, le diagramme qui représente le métabolisme cellulaire n’a pas besoin de représenter en détails l’apparence de la cellule, il lui suffit d’inclure les différentes parties (enveloppe, noyau, cytoplasme) qui jouent un rôle dans le processus qu’il souhaite expliquer (par exemple, la division cellulaire. Pour éclairer notre propos, analysons deux diagrammes présents dans Flatland, le premier page 10 et le second page 56 de notre édition. Malgré la distance qui les sépare dans l’œuvre, ces deux diagrammes présentent une structure tout à fait similaire : ils proposent une représentation visuelle d’un mouvement, d’un déplacement au cours du temps signalé par la numérotation de trois étapes. Pour le premier, il s’agit d’un changement de point de vue qui figure le passage d’une vision en trois dimensions à une vision en deux dimensions, c’est-à-dire comment on « voit » un triangle du point de vue de Flatland. Le second schéma représente la « disparition » progressive de la sphère qui quitte le champ de vision d’un habitant flatlandien, et ce que ce dernier voit durant ces différentes étapes, à savoir un cercle de plus en plus petit qui se rétrécit jusqu’à former un point et disparaître complètement.

Figure 4 : Un triangle vu du point de vue de Flatland (Abbott, 2007, p.10)

Figure 5 : Une sphère vue du point de vue de Flatland (Abbott, 2007, p. 56)

Dans ces deux cas, la représentation visuelle et diagrammatique qui est proposée au lecteur permet de :

• Confronter les points de vue d’observateurs de la troisième et de la deuxième dimensions en les superposant dans un schéma en deux dimensions

• Représenter en deux dimensions un mouvement, c’est-à-dire un changement de position dans l’espace au cours du temps, d’un objet en deux dimensions pour le premier schéma et en trois dimensions pour le second

• Proposer de façon sous-jacente un axe temporel, ce qui permet d’inclure le temps dans l’étude des dimensions

Ces représentations diagrammatiques présentent l’intérêt de pouvoir superposer ces différentes couches de sens et d’autoriser des comparaisons à différentes échelles et sur différents aspects. Il nous faut systématiquement garder en tête le fait qu’A. Square, lui, n’a pas accès à ces représentations afin de faciliter sa compréhension de la situation – d’autant plus qu’elles obéissent à des règles de perspectives propres à une vision en trois dimensions, quand bien même il s’agisse de représentations en deux dimensions. Ainsi, Flatland regorge d’une multitude de diagrammes qui permettent au lecteur de se plonger et de se représenter une vision du monde en deux dimensions, et donc de penser les articulations avec une dimension supérieure. Le savoir mathématique qui nous est transmis dans l’œuvre repose en grande partie sur ces outils visuels : il y a fort à parier qu’une simple description du mouvement de la sphère qui apparait du plafond d’une maison dans un monde à deux dimensions, formant au regard de l’habitant qui l’observe un point, puis un cercle grossissant, puis diminuant progressivement jusqu’à redevenir un point et disparaître, aurait été bien plus ardue à comprendre pour un lecteur néophyte sans la présence du diagramme qui l’accompagne.

La représentation visuelle et notamment diagrammatique est donc indéniablement un outil fécond dans la transmission du savoir. Elle vient accompagner le raisonnement et en l’occurrence ici la représentation de ce que peuvent être des mondes à n dimensions. Elle a toutefois, bien évidemment, ses limites : si nous suivons l’invitation d’A. Square à tenter d’envisager ce que peut être la quatrième dimension, nous nous heurtons bien évidemment à de nombreux problèmes épistémiques. Il nous est par exemple possible de dessiner un objet de quatrième dimension, l’hypercube, en suivant le raisonnement analogique développé dans Flatland, sans être nécessairement capable de le comprendre ou de se le représenter véritablement …

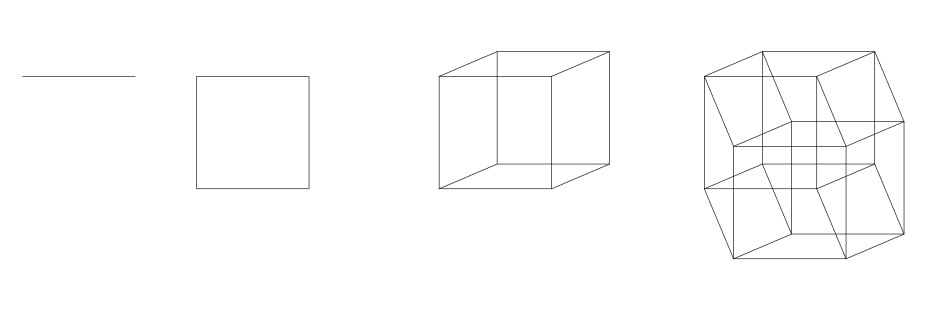
Figure 6 : De la ligne à l'hypercube

3. Quand les mathématiques font signe vers l’inconcevable

Edwin A. Abbott est un mathématicien, mais aussi et également un théologien. Il a donc cherché dans ses écrits à concilier ces deux facettes de sa formation, qui n’en font à ses yeux qu’une, et nous allons voir comment.

Dans son article « The Fourth Dimension and the Theology of Edwin Abbott Abbott » (Banchoff, 1989) Thomas F. Banchoff revient sur le problème que soulève le sens des mots convoqués dans un espace autre, déterritorialisés en quelque sorte : « How do we express the ineffable in words ? The theologian and the mathematician share the same problem: the dimensional analogy is an attempt on the part of mathematicians to explain situations in which our words no longer mean the same thing »⁶. À titre d’exemple, il mentionne l’emploi des prépositions utilisées pour les déplacements d’A. Square dans sa maison : « across », « behind », « between », « in » qui bien évidemment n’ont pas du tout la même signification pour nous que pour le narrateur qui se déplace dans un monde à deux dimensions. Pour Banchoff, les prépositions, étant donné leur caractère relationnel et transitifs, sont les mots les plus « dimensionnels » de notre langage. Penser une autre dimension, concevoir par l’imagination un autre axe de l’espace et tenter de se projeter dans l’espace selon cet axe que l’on ignore totalement, est donc une expérience de pensée propre à soulever un certain nombre de problèmes sémantiques. Les difficultés épistémiques qui en résultent conduisent souvent les personnages de Flatland à envisager un espace autre, en lieu et place d’un axe de l’espace différent. Ainsi, le roi de Lineland explique : « Though he had heard my voice when I first addressed him, the sounds had come to him in a manner so contrary to his experience that he had made no answer, “seeing no man”, as he expressed it, “and hearing a voice as it were from my own intestines”⁷ » (Abbott, 2007, p. 44) . Il parle de son « intérieur » en réintroduisant une dialectique entre le dedans et le dehors puisqu’il ne lui est pas possible de concevoir le plan sur lequel se situe A. Square. Nous retrouvons donc dans le texte d’Abbott cette idée d’une impuissance à saisir par les mots une réalité complexe, qui relève en quelque sorte de l’indicible en ce qu’elle bouleverse nos catégories langagières. Peut-on montrer, démontrer ou même concevoir ce que l’on ne parvient pas à dire ? C’est une question que soulève la théologie aussi bien que les mathématiques, et en ce sens, le récit fictionnel sur ce monde à deux dimensions, les dialogues, les diagrammes qui l’accompagnent, forment en quelque sorte un pendant aux paraboles religieuses et aux textes sacrés.

Nous pouvons même aller plus loin en affirmant que cette réflexion sur les mondes à plusieurs dimensions constitue en elle-même un argument théologique propre à prouver l’existence de Dieu. Pour cela, revenons sur l’illustration de la couverture de Flatland que nous avions déjà analysée. Il existe deux versions de l’illustration de la couverture originelle (selon que la maison de A. Square apparaisse ou non), qui figurent toutes deux les différentes dimensions : pointland (pas de dimension), lineland (une dimension), flatland (deux dimensions), spaceland (trois dimensions). Au-dessus se déploie un grand nuage qui masque potentiellement les autres dimensions mystérieuses. La seule différence importante entre les deux couvertures est la citation qui figure en bas : « Fie, fie, how frantically I square my talk » sur l’une (tirée de Titus Andronicus et qui vraisemblablement sert surtout à introduire un jeu de mot avec la figure du carré), « And therefore as a stranger give it welcome » sur la version plus élaborée. Cette seconde citation, extraite d’Hamlet, est moins connue que les deux vers qui la suivent : « There are more things in heaven and earth, Horatio / Than are dreamt of in your philosophy ». Selon Snezana Lawrence et Mark McCartney, cette citation fait allusion à l’argumentaire d’Abbott et au lien qu’il souhaite établir entre discours mathématique et religion :

Abbott’s argument is that, now that geometers have demonstrated that other worlds can exist, Christians have to reassess the basis of their beliefs. Geometers have proved that a fourth dimension may be out there, as real as the three we can see around us. If they are right, and this is not an abstract theoretical concept but a concrete reality, there may be creatures living there that could be in contact with our world, like the Sphere in Flatland⁸(Lawrence et McCartney, 2015).

Lawrence et McCartney voient dans cette démonstration de l’existence d’une quatrième dimension un argument également théologique qui vient souligner qu’il est possible de concevoir par l’esprit des objets dont l’existence est prouvée mais non perceptible – cette dimension plus religieuse étant elle aussi suggérée par les cieux figurés sur l’image de couverture. La quatrième dimension offre une image puissante propre à bouleverser nos représentations du monde, dont A. Square a pleinement conscience lorsqu’il se compare à Prométhée :

Prometheus up in Spaceland was bound for bringing down fire for mortals, but I – poor Flatland Prometheus – lie here in prison for bringing down nothing to my countrymen. Yet I exist in the hope that these memoirs, in some manner, I know not how, may find their way to the minds of humanity in Some Dimension, and may stir up a race of rebels who shall refuse to be confined to limited Dimensionality⁹ (Abbott, 2007, p.76)

Pour le dire autrement, puisque le raisonnement mathématique nous permet d’envisager – et même de prouver – l’existence de mondes à plus de trois dimensions, qui restent pourtant inaccessibles à notre expérience première, nous pouvons de façon tout à fait analogue postuler l’existence de Dieu, celle-ci ne pouvant être remise en question par l’absence d’expérience sensible. Le parallèle est tout à fait probant, puisqu’à la fin de l’œuvre, A. Square nous parle de ceux qui « croient » en la troisième dimension, puisque depuis Flatland, c’est la seule attitude épistémique possible.

Conclusion

Pour conclure, ce petit détour par le monde – ou plutôt les mondes – de Flatland nous aura permis d’aborder un certain nombre d’enjeux liés au savoir mathématique, en montrant comment la littérature peut s’emparer de certaines questions et quelles réponses elle peut proposer. L’œuvre d’Edwin A. Abbott regorge de situations qui nous amènent à interroger les modalités de transmission du savoir, que ce soit à l’intérieur de l’intrigue entre les personnages, mais aussi en dehors dans un face à face avec le lecteur qui est constamment impliqué et auquel l’œuvre est directement adressée. Ce savoir a une dimension éminemment politique puisqu’il régit le fonctionnement du monde fictionnel de Flatland. Enfin, Abbott tisse un lien entre son propos mathématique et un propos plus théologique. Dans The Kernel and the Husk, une série de lettres adressées à un sceptique qui traverse une période de crise dans sa foi religieuse, Abbott développe une métaphore tout à fait intéressante que Banchoff résume ainsi : « The beauty of Scripture comes wrapped in parables, in stories. The education of the individual and of the race is to remove gradually this hull, this husk, from the kernel¹⁰ » (Banchoff, 1989). Abbott souhaite donc transmettre ce « noyau », qui représente la vérité (à la fois religieuse et mathématique), débarrassé de la coque qui l’encombre et le dissimule à la manière du nuage qui flotte sur le frontispice de la première édition de Flatland. Pourtant, on ne peut s’empêcher de voir également dans ces lignes un amour et un goût pour ces enveloppes successives qui l’entourent, ces histoires et ces paraboles qui sont un des chemins possibles vers un noyau que l’on n’atteint peut-être jamais véritablement.

Bibliographie

Abbott Edwin Abbott, Flatland: a romance of many dimensions, Teddington, Middlesex, Echo Library, 2007.

Abbott Edwin Abbott, The Kernel and the Husk, Londres, Macmillan & Co, 1886.

Banchoff Thomas, « The fourth dimension and the theology of Edwin Abbott Abbott », dans Seventh Conference on Mathematics from a Christian Perspective, Wheaton, États-Unis, Wheaton College Mathematics Department, 1989.

Marot Patrick (éd.), L’inscription littéraire des savoirs, Paris, France, Classiques Garnier, 2019.

Lawrence Snezana et Mark McCartney, Mathematicians and their Gods: Interactions between mathematics and religious beliefs, Oxford, OUP Oxford, 2015.

McLuhan Marshall et Jean Paré, Pour comprendre les médias: les prolongementstechnologiques de l’homme, Paris, France, Seuil, 2000.

Minary Daniel (éd.), Savoirs et littérature. II, Besançon, France, Presses universitaires franc-comtoises, 2001.

Peirce Charles Sanders, Collected papers, Charles Hartshorne et Paul Weiss (éd.), Cambridge, Mass., Etats-Unis d’Amérique, Harvard University Press, 1931, 8 vol.